
このページは約 7 分で読めます。有意義なページになっていますので、最後までご覧ください。
目次
中学1年生で学ぶ「比例(ひれい)」は、数学の基礎となる重要な単元です。
しかし、「比例」の概念は、生徒によって得意不得意が大きく分かれる部分でもあります。
比例を得意単元にすることができれば、テストで大きく成績をアップしていくことも可能です。
そこでこの記事では、「比例ってなに?」という基本的な疑問に答えながら、比例の基本的な考え方をわかりやすく解説していきます。
例題や練習問題も取り入れながら説明していきますので、是非一緒に勉強しましょう。
比例ってなに?
まずは「比例」とは何かを説明します。
比例とは、2つの数が互いに関係して変化することの表し方の一つです。
一方の数が増えると、もう一方も一定の割合で増える関係を「比例」と呼びます。
例えば、自動販売機でジュースを買うとき、ジュース1本が120円だとします。
2本買えば240円、3本買えば360円です。
このように、本数が増えるごとに料金も同じ割合で増えるような関係が「比例」の典型例です。
ジュースの本数:1本→2本→3本
ジュースの金額:120円→240円→360円
【ワンポイントアドバイス】
比例関係にある2つの数量の関係は、グラフにすると一直線になります。この直線のことを「比例のグラフ」と呼びます。
比例の式
比例の関係は、数学では次のような「比例の式」で表されます。
y = ◯x
◯は比例定数(ひれいていすう)と呼ばれる値です。
xが増えるとyがどれだけ増えるかを示す値です。
例えば、比例定数が2であれば、xが1増えるごとにyは2増えるという意味になります。
【例】
xが1増えるごとにyが3増えるときの比例の式は「y = 3x」です。
このように、比例定数「◯」を求めることで、xとyの関係を数式で表すことができます。
比例のグラフ
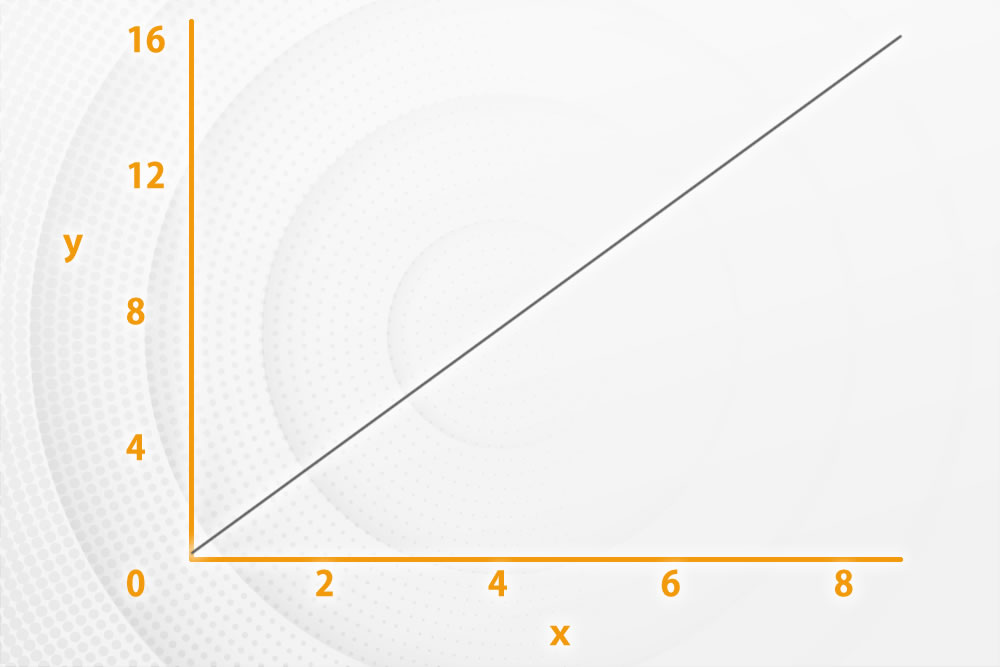
比例の関係をグラフで表すと、xとyの関係が直線になります。
この直線は必ず原点(0, 0)を通り、右上がりの直線になります。
このグラフを見ると、xが増えるにつれてyも「比例」して増えることが一目でわかります。
【例】
y = 2x という比例のグラフを描いてみましょう。
例えば、xが1のときyは2、xが2のときyは4です。
これらの点を結ぶと、原点を通る右上がりの直線が得られます。
この直線の傾きが比例定数「◯」であり、グラフからも比例定数の大きさを理解することができます。
比例の例題で理解を深めよう比例について、具体的な例題を使って理解を深めてみましょう。
例題1:比例の式を求める問題
「りんご1個の値段が150円です。りんごの個数をx、料金をyとしたとき、yとxの関係を比例の式で表しましょう。」
この問題では、りんごの個数xに対して料金yが比例しています。
1個あたり150円なので、比例定数は150です。
そのため、比例の式は次のようになります。
y = 150x
【ワンポイントアドバイス】
りんごの数(x)が1増えるたびに、料金(y)が150ずつ増えていきます。
りんご1個の時:料金150円
りんご2個の時:料金300円(150円アップ)
りんご3個の時:料金450円(150円アップ)
例題2:比例のグラフを描く
次に、比例のグラフを描く練習をしてみましょう。
「y = 3x の比例のグラフを描いてみましょう。」
この式では、比例定数が3なので、xが増えるごとにyは3倍に増えます。
例えば、xが1のときyは3、xが2のときyは6です。
これらの点を結ぶと、原点を通り右上がりの直線になります。
この直線が「y = 3x」の比例のグラフです。
比例と反比例の違い
中学1年生で学ぶもうひとつの重要な単元として、「反比例(はんぴれい)」があります。
比例と反比例は対になるような関係があります。
比例と反比例の違いについても簡単に理解しておきましょう。
比例:一方の量が増えると、もう一方も一定の割合で「増える」関係。
反比例:一方の量が増えると、もう一方が逆に「減っていく」関係。
比例では「y = ◯x」の形をしていましたが、反比例の場合は「y = ◯/x」という形になります。
この違いを理解しておくと、次に学ぶ反比例も理解しやすくなります。
練習問題
1. 1冊200円のノートがあります。このノートをx冊買ったときの料金yを比例の式で表しなさい。
2. y = 5x のグラフを描いて、xが1, 2, 3のときのyの値を求めなさい。
3. y = 4x のとき、xが3のときyはいくらですか?
答え:
1. y = 200x
2. x = 1のときy = 5, x = 2のときy = 10, x = 3のときy = 15
3. y = 4 × 3 = 12 y=12
比例をもっと簡単に学びたい生徒は代々木個別指導学院に相談!

比例は数学の基礎であり、この先の数学の学習にもつながる非常に重要な部分です。
もし、比例の意味や使い方にまだ不安がある生徒は、代々木個別指導学院で一緒に勉強しましょう。
代々木個別指導学院では、生徒一人ひとりに合わせた「キミ専用カリキュラム」を作成し、生徒の理解度や目的に応じた、わかりやすく丁寧な指導を行っております。
比例や数学が苦手な生徒でも、確実に成績アップにつなげることができます。
無料体験授業やカウンセリングも実施中ですので、ぜひお気軽に、代々木個別指導学院までお問い合わせください。
代々木個別指導学院は東京都、神奈川県、埼玉県、千葉県に85校あります。







とは.jpg)









